Памятники – это не просто каменные сооружения, они олицетворяют вечность и память о прошлом. А если эти памятники созданы из гранита, они не только красивы и величественны, но
Женские платья – это не просто одежда, это история, самовыражение и возможность почувствовать себя прекрасной и уверенной. Платье, будь то вечернее, повседневное или деловое, имеет магическую силу притяжения
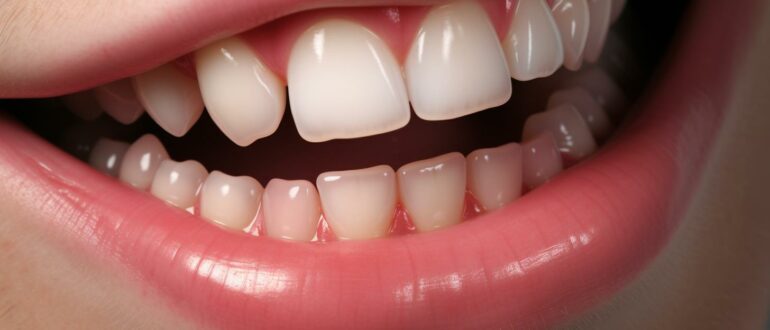
Введение Здоровье наших зубов играет важную роль в общем состоянии организма и нашей самооценке. К сожалению, проблемы с зубами неизбежны, но правильный уход и своевременное лечение могут минимизировать
Педикюр – важная часть нашей ежедневной гигиены. Красиво и ухоженно то, что наши ноги выглядят привлекательно и здорово. Правильный выбор товаров для педикюра – залог красоты и здоровья
Ремонт квартир – это процесс, который может быть как захватывающим, так и утомительным. В конечном итоге, все мы стремимся превратить наше жилище в уютное гнездо, отражающее нашу индивидуальность.
7 признаков, что пора к мастеру Холодильник не морозит: Это самый очевидный признак поломки. Если продукты не охлаждаются, а температура в камерах выше нормы, необходимо срочно вызвать мастера.
Мы живем в удивительное эпоху, когда мир все более объединен и границы между странами становятся все меньше значимыми. Международное обучение становится все более популярным и востребованным, предлагая уникальную
Введение Свадьба – это особое событие в жизни каждого человека. И пусть главными героями в этот день являются молодожены, не менее важную роль играют гости, которые присутствуют на
Душевая кабина с инфракрасной сауной – это современное решение, которое сочетает в себе комфорт и пользу для вашего организма. Это уникальное сочетание позволяет вам расслабиться и получить заряд